It is a bright Spring morning. You have just been to a calculus class, and are feeling very good about yourself. You are especially proud that you have just learned how to solve separable differential equations, and are reasonably confident that you understand why the method works. As you leave the building, a wild-eyed, hungry-looking stranger stops you on the street. "I know you!'' he shouts. "You always come around here toting your fancy Calculus book, filled with its junk. You could read that book all day and it wouldn't flip a single flapjack, do you hear me? Not a single flapjack.''

You aren't sure how to respond, but you try anyway. "This book is NOT filled with 'junk.' For example, today I learned how to solve differential equations by separation of variables - a powerful method almost beautiful in its simplicity.''

The stranger's face turns from a scowl to a condescending smile. "There ya go! You'll swallow anything your teachers tell you. Tell me this. Is the differential equation separable? Even if we have the initial condition y(0) = 0?

"Why, certainly'' you reply.

"Well then, smarty, feast your peepers on THIS!'' he concludes triumphantly, and hands you a piece of paper with the following written on it:

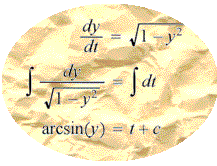
After you've had about 3 seconds to look at it, he says, "And since y(0) = 0, we have that c = 0! Then we get, as our final answer, y = sin(t)"

"Yes..." you say.

"Yo ho!" he replies. "There are values of t for which cos(t) is negative, but ; is never negative! So all you learned today was lies! Lies!''

Is the stranger correct? Are you positive? Is he being too negative? But then again, if he is right, those words don't really have any meaning at all! The fate of the real number line is in your hands. Find the error.

Back to Find The Error!
Go to Doug Shaw's Professorial page

Doug Code: mdkx wftvkn pbohhkn: "o hcm'b vqncpk tu lifgqb'p pfhhomhbru kmifgq bi sob im c" -eifg pqcx

Copyright 2001 by Douglas Shaw